Inferential Statistics(12)-Non-parametric tests

1. Non-parametric statistics

t-test
- to compare 2 independent means
  - Assumptions
    - independent observations(random assignment/selection)
    - normally distributed?(one-sided test) (usually > 30)
ANOVA
- A quantitative response variable has a categorical explanatory variable.
  - Assumptions
    - Independent random samples(random sampling or a randomized experiment)
    - normal population distributions with equal standard deviations.(n in each group ≧ 10)
t-test vs. ANOVA
1. t-test 只关注两组样本直接的差异。ANOVA关注多个样本。
2. t-test 假设两组样本均值相等，置信区间为两组差值范围。 ANOVA假设factor(Categorical variable)导致多个样本组均值，置信区间可用t-test计算.
3. t-test为t分布。ANOVA为F分布。
Non-parametric statistics
- do not assume a particular form of distribution, such as the normal distribution, for the population distribution.
  - 对于总体/样本正态性未知或非正态分布
    - 小样本<20
    - 排列参数（Ordinal/rank）
  - 正态分布检验

2. Wilcoxon Test: Comparing Mean Ranks(Two independent samples)

The test comparing two groups based on the sampling distribution of the difference between the sample mean ranks.

Assumptions
- Independent random samples from two groups
  - random sampling
  - randomized experiment
Hypotheses:
- \[H_0= Identical\ population \ distributions \ for \ the \ two \ groups \\ (this \ impllies \ equal \ population \ mean \ ranks.)\]
- \[H_a = Different \ population \ mean \ ranks \ (two-sided) \\ H_a = Higher \ population \ mean\ rank\ for \ a \ specified \ group \ (one-sided)\]
Test statistic:
- Difference between sample mean ranks for the two groups
P-value
- One-tail or two-tail probability depending on Ha, that the difference between the sample mean ranks is as extreme or more extreme than observed.
Conclusion
- Interpret in context

3. Large-Sample P-Value Use a Normal Sampling Distribution(Z-test)

Using the normal distribution for the large-sample(n>20) test does not mean we are assuming that the normal distribution for the response variable has a normal distribution. We are merely using the fact that the sampling distribution for the test statistic is approximately normal.

Z-test \(z = (difference\ between \ sample \ mean \ ranks)/ se\)
P-Value
- Asymp.Sig.(two-tailed)

4. Nonparametric Estimation(CI) Comparing Two Groups

Additional assumption
- the population distributions for the two groups have the same shape.
Point estimate for group difference

5. Wilcoxon rank-sum test(Mann-Whitney U test) (Two independent samples)

U-test
- where R1 = sum of the ranks for group 1 and R2 = sum of the ranks for group 2.
In every test, we must determine whether the observed U supports the null or research hypothesis. This is done following the same approach used in parametric testing. Specifically, we determine a critical value of the smaller U such that if the observed value of U is less than or equal to the critical value, we reject H0 in favor of H1 and if the observed value of U exceeds the critical value we do not reject H0.
U-table

6. Kruskal-Wallis Test: Comparing mean ranks of several group

Assumptions:
- Independent random samples from several groups, either from random sampling or a randomized experiment.
Hypotheses:
- \[H_0: Identical \ population \ distributions \ for \ the \ g \ groups \\ H_a: Population \ distributions \ not \ all \ identical\]
Test statistic:
- Uses between-groups variability of sample mean ranks
- \[K=(\frac{12}{n(n+1)})\sum n_i(\overline{R_i}-\overline{R})^2\]
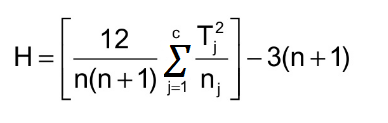
- - Ri = sample mean rank
  - R = the combined sample mean of g groups
  - n = total number of data points
  - df = g-1
P-value
- test statistic value from chi-squared distribution with df=g-1
- chi-square table
Conclusion
- If the P-value is small, to find out which pairs of groups significantly differ, we could follow up the Kruskal-Wallis test by a Wilcoxon test to compare each pair.

7. Sign test: Comparing Matched Pairs(Dependent samples)

Assumptions
- Random sample of matched pairs for which we can evaluate which observation in a pair has the better response.
- pretend the equal data points do not exist
Hypotheses
- \[H_0: Population \ proportion \ p \ = \ 0.5 \\ H_a: \ p ≠ 0.5 \ (two -sided) \\ or \ H_a: \ p> 0.5 \ or \ p<0.5 \ (one-sided)\]
Test statistic
- \[Z = \frac{(\hat{p}-0.5)}{se} \\ se = \sqrt{(0.5)(0.5)/n}\]
P-value
- for large samples(n>30), use tail probabilities from standard normal. (z-score)
- for smaller n, use binomial distribution
  - \[P(x)=\frac{n!}{x!(n-x)!}p^x(1-p)^{n-x}\]
  - binomial distribution table

8. Wilcoxon Signed-Rank test: Ranking and Comparing Matched Pairs(Dependent samples)

Assumption
Random sample of matched pairs for which the differences of observations have a symmetric population distribution and can be ranked.
Hypotheses
- \[H_0: Population \ median \ of \ difference \ socres \ is \ 0 \\ H_a: Population \ median \ of \ difference \ scores \ in \ not \ 0 \ (one-sided \ also \ possible)\]
Test statistic
- Rank the absolute values of the difference scores for the matched pairs
- find the sum of ranks for those differences that were positive
P-value
- a P-value based on all the possible samples with the given absolute differences
- for large samples, it uses an approximate normal sampling distribution.
Conclusion
- the smaller W such that if the observed value of W is less than or equal to the critical value, we reject H0 in favor of H1 and if the observed value of W exceeds the critical value we do not reject H0.
Notes:
- Because of Wilcoxon signed ranks test’s extra assumption of Symmetry, many statisticians prefer to use the matched pairs t test for such data.
- How to select the right t-test to compare two sample means?

9. Spearman ranked correlation

Correlation coefficient = standardized measure of association

Pearson	Spearman
Parametric	Non-parametric
[-1,1]	[-1,1]
1. linear association 2. variables are bivariate normally distributed 3.sensetive to outliers and skewedness	1. non -linear association 2. measures strength of monotonic function(单调函数) 3. ordinal variable 4. can contain outliers 5. non-normal distribution is okay

10. Runs Test for Randomness

A runs test is a statistical procedure that examines whether a string of data is occurring randomly from a specific distribution. The runs test analyzes the occurrence of similar events that are separated by events that are different.

A run is a succession of identical values or labels which are followed and preceded by different values or labels.
two variation form
run test properties
- only consider binominal data
- numerical data
  - values above/below mean
  - increasing/decreasing values
- more than two categories
  - aggregate to two
- ordering is crucial
  - don’t re-arrange data
runs test

count number of runs in the data.
- group sizes: m or n <10 probability table
- m or n > 10 z-test
  - - total sample size N = m + n